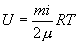Тема 8."Основы молекулярно-кинетической теории газов"
ВведениеЗадача молекулярно–кинетической теории – вывести все свойства вещества из его молекулярно-кинетической модели. Модель эта содержит представления о свойствах молекул вещества, их движении и взаимодействии. Представления, естественно, уточняются с развитием науки, поэтому уточняется и модель. Основные положения этой модели следующие:
Следует заметить, что внутренняя структура самой молекулы описывается квантовой физикой. Включение в описание явлений внутреннего строения молекул, является дальнейшим уточнением модели. 10.1 Основное уравнение м.к.т. идеальных газов. ТемператураТак принято называть выводимое из м.к.т. уравнение, определяющее давление газа. Важным здесь является выяснение молекулярно-кинетического понятия температуры. Для дальнейшего нам понадобится понятие концентрации молекул. Будем называть концентрацией n число молекул в единице объема.
Первая формула справедлива всегда, вторая – в случае, если концентрация всюду в объеме постоянна. Через концентрацию можно выразить и давление газа 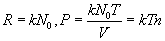 . .
Необходимо вывести это же уравнение из молекулярно-кинетической теории, иными словами, найти давление газа на стенку. Давление – результат ударов молекул. Импульс, переданный всеми молекулами за секунду, – это и есть сила давления т.е. PS, где S – площадь стенки. Поскольку при каждом соударении молекул полный импульс сохраняется, для расчета давления не нужно учитывать соударения молекул между собой. 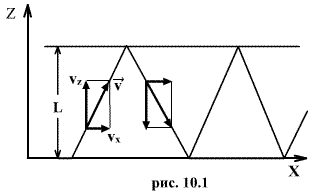 Рассмотрим молекулу (рис.10.1), движущуюся между стенками сосуда, расстояние между которыми L. При ударе о верхнюю стенку меняется только составляющая скорости Изменение импульса молекулы при ударе (т.е. передаваемый стенке импульс) равно δp=2mvz . Это изменение импульса приходится на время Итак, средняя сила, действующая со стороны одной молекулы на стенку, равна 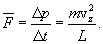 У разных молекул разные скорости, поэтому вместо 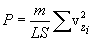 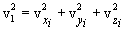 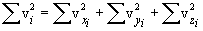 Ввиду равноправия осей x,y,z при т.д.р. три суммы справа должны быть (при большом числе молекул) равны между собой, откуда 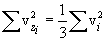 . .Введем понятие среднеквадратичной скорости (она называется еще тепловой скоростью vi ). Для этого необходимо найти средний квадрат скорости. Он, очевидно, равен
Выражение (10.3) вполне аналогично выражению для средней арифметической скорости
Среднеквадратичной, или тепловой скоростью называется корень квадратный из выражения (10.3):
Заметим, что Возвращаясь к выводу уравнения м.к.т. газов, запишем, пользуясь уравнением (10.3): 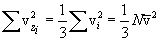 . .Подставляя полученное выражение в выражение для P, получим 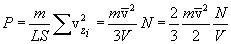 . .Наконец, учитывая, что 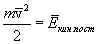 есть средняя кинетическая энергия поступательного движения молекул, получим
Это и есть основное уравнение м.к.т. идеальных газов. Оно читается так: давление газа равно Сравнивая (10.6) с (10.2), получим очень важное равенство
Это выражение объясняет молекулярно-кинетический смысл понятия температуры. Температура – это средняя кинетическая энергия движения молекул (выраженная в других единицах). В этом определении очень важным является слово «средняя». Если изъять из газа наиболее медленные молекулы, полная кинетическая энергия всех молекул уменьшится, но температура повысится, так как увеличится средняя энергия. Записывая
Эта скорость пропорциональна корню квадратному из температуры. Можно записать (10.9) в виде
Для молекулы кислорода (μ=0,032 кг/моль) при Т=300К 483 м/с. Для молекулы водорода (μ=0,002 кг/моль) при этой же температуре скорость равна vТ=1932 м/с, т. е. она больше, чем у молекулы кислорода, в 4 раза. Весьма важным является то обстоятельство, что в условиях т. д. р., которые рассматриваются, средняя кинетическая энергия молекулы (10.8) не зависит от массы молекулы. Если мешать несколько газов, например Н2, О2 и газ с молекулами, в сотни раз более тяжелыми, чем молекулы водорода, то при условии, что смесь будет находиться в состоянии т. д. р., средняя кинетическая энергия молекул всех газов будет одинакова. Тяжелые молекулы будут двигаться с малыми скоростями, такими, чтобы их средняя кинетическая энергия как раз равнялась энергии легких молекул. Средняя кинетическая энергия броуновых частиц в жидкости, несмотря на огромную (по сравнению с молекулами) массу этих частиц, такая же, как у молекул. Можно рассматривать тяжелый и легкий газ как две системы, находящиеся в т. д. р. друг с другом. Термодинамическое равновесие предполагает равенство температур этих систем. Иначе тепло будет передаваться от более горячей системы к более холодной. 10.2 Распределение энергии по степеням свободы молекулы.Молекулы можно рассматривать как системы материальных точек (атомов) совершающих как поступательное, так и вращательное движения. При исследовании движения тела необходимо знать его положение относительно выбранной системы координат. Для этого вводится понятие о степенях свободы тела. Число независимых координат, которые полностью определяют положение тела в пространстве, называется числом степеней свободы тела. При движении точки по прямой линии для оценки ее положения необходимо знать одну координату, т.е. точка имеет одну степень свободы. Если точка движения по плоскости, ее положение характеризуется двумя координатами; при этом точка обладает двумя степенями свободы. Положение точки в пространстве определяется 3 координатами. Число степеней свободы обычно обозначают буквой i. Молекулы, которые состоят из обычного атома, считаются материальными точками и имеют три степени свободы (аргон, гелий). 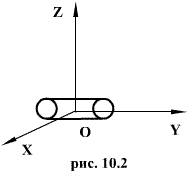 Двухатомные жесткие молекулы, например молекулы водорода, азота и др., обладают пятью степенями свободы: они имеют 3 степени свободы поступательного движения и 2 степени свободы вращения вокруг осей ОХ и OZ. Вращением вокруг оси OY можно пренебречь, т.к. момент инерции ее относительно этой оси пренебрежимо мал. Поэтому вклад энергии вращательного движения вокруг оси OY в суммарную энергию двухатомной молекулы можно не учитывать. Молекулы, состоящие из трех и более жестко связанных атомов, не лежащих на одной прямой, имеют число степеней свободы i = 6: три степени свободы поступательного движения и 3 степени свободы вращения вокруг осей ОХ, OY и OZ. В этом случае, если расстояние между атомами может изменяться (нежесткие молекулы), появляются дополнительные степени свободы . Согласно молекулярно-кинетической теории газов движение молекул носит беспорядочный характер; эта беспорядочность относится ко всем видам движения молекулы. Ни один из видов движения не имеет преимущества перед другим. При статистическом равновесии движений энергия в среднем распределяется равномерно между всеми видами движения. Закон равномерного распределения энергии по степеням свободы молекул можно сформулировать следующим образом: статистически в среднем на каждую степень свободы молекул приходится одинаковая энергия. Поступательное движение молекул характеризуется средней кинетической энергией, равной 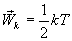 В однородном газе, молекулы которого имеют любое число степеней свободы i, каждая молекула в среднем обладает энергией движения, равной
10.3 Внутренняя энергия идеального газа.В теории идеального газа потенциальная энергия взаимодействия молекул считается равной нулю. Поэтому внутренняя энергия идеального газа определяется кинетической энергией движения всех его молекул. Средняя энергия движения одной молекулы равна 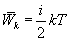 Так как в одном киломоле содержится 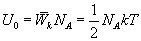 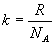 , получим , получим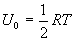 Для любой массы m газа, т.е. для любого числа киломолей
Из этого выражения следует, что внутренняя энергия является однозначной функцией состояния и, следовательно, при совершении системой любого процесса, в результате которого система возвращается в исходное состояние, полное изменение внутренней энергии равно нулю. Математически это записывается в виде тождества 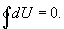 |
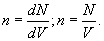
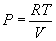 . Используя введенную ранее постоянную Больцмана
. Используя введенную ранее постоянную Больцмана 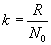 запишем
запишем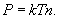
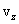 . Эта составляющая меняется на
. Эта составляющая меняется на 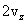 .
.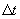 , протекающее между двумя ударами о верхнюю стенку, которое равно
, протекающее между двумя ударами о верхнюю стенку, которое равно 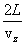 .
.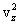 надо записать
надо записать 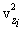 , где i – номер молекулы. Полная сила со стороны всех молекул
, где i – номер молекулы. Полная сила со стороны всех молекул 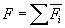 . Для того чтобы найти давление, нужно эту силу разделить на площадь стенки S:
. Для того чтобы найти давление, нужно эту силу разделить на площадь стенки S: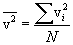
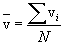
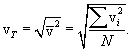
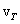 всегда больше средней арифметической скорости (10.4). Это легко проверить, подставляя вместо
всегда больше средней арифметической скорости (10.4). Это легко проверить, подставляя вместо 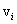 любые (неравные) числа.
любые (неравные) числа.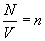 - концентрация, и замечая, что
- концентрация, и замечая, что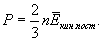
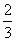 кинетической энергии поступательного движения молекул, заключенных в единице объема.
кинетической энергии поступательного движения молекул, заключенных в единице объема.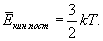
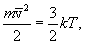
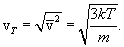
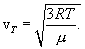
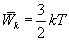 . Так как поступательному движению соответствует 3 степени свободы, то в среднем на одну степень свободы движения молекул приходится энергия
. Так как поступательному движению соответствует 3 степени свободы, то в среднем на одну степень свободы движения молекул приходится энергия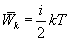
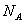 молекул, то внутренняя энергия одного киломоля газа будет
молекул, то внутренняя энергия одного киломоля газа будет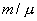 внутренняя энергия
внутренняя энергия