Тема 6: "Специальная теория относительности."
|
Уже в динамике Ньютона четко сформулировано выделение движения по инерции среди всех остальных движений. Прямым логическим следствием из первого закона Ньютона является утверждение, что все инерциальные наблюдатели равноправны - в той степени, в какой справедлив первый закон Ньютона. Согласно вполне правдоподобному умозаключению, равноправие наблюдателей распространяется на все другие законы движения и, следовательно, на все другие механические явления. Эйнштейн же распространил это равноправие на все явления вообще, сформулировав знаменитые постулаты: 1. Все физические законы инвариантны по отношению к переходу от одной инерциальной системы отсчета к другой. 2. Скорость света в вакууме равна одной и той же величине во всех системах отсчета и не зависит ни от скоростидвиженияисточника, ни от скоростидвиженияприемника. 6.1. Преобразования ЛоренцаИсходя из сформулированных выше постулатов теории относительности Эйнштейна, можно найти законы преобразований, связывающие межу собой пространственные координаты и время в двух системах отсчета, движущихся прямолинейно и равномерно относительно друг друга. 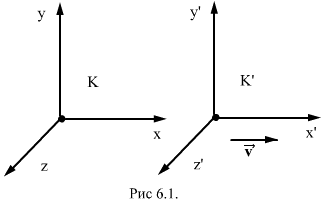 Пусть х, у, z, и х', у', z' и t',- координаты и время в инерциальных систем отсчета K и K', а v - скорость их относительного движения (рис. 6.1). При этом нет никаких оснований полагать, что время в системе 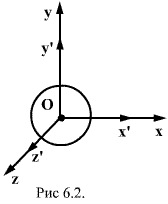 Выберем за начало отсчета времени t=0 тот момент, в который начало координат системы K' совпадало с началом координат системы K. Пусть в момент времени t=0 из начала координат начала распространяться сферическая электромагнитная волна (рис.6.2). В системе K уравнение волновой поверхности имеет вид.
или
Поскольку, согласно принципу относительности Эйнштейна, закон и величина скорости распространения волны должны быть одинаковыми во всех инерциальных системах отсчета, наряду с этим уравнением с равным правом можно написать уравнение сферической волны в системе K'.
Так как в начальный момент времени начало координат систем совпадали, то
Формулы преобразования координат и времени должны, во-первых, не нарушать соотношений (6.1) и (6.2), а, во-вторых, быть линейными. Требования линейности связано с однородностью пространства. Т.к. движение системы K' происходит только вдоль оси х преобразование координат у и z должно иметь вид
Закон преобразования х' через х можно написать, исходя из следующегосоображения: если в момент времени t=0 начала систем координат K и K' совпадали, то координата плоскости х' в системе K запишется х=νt. Следовательно, в самом общем случае можно написать
где коэффициент
Kоэффициенты
Для выполнения тождества необходимо приравнять коэффициенты при х2,t2и хt. Раскрыв скобки и проведя соответствующие преобразования получим:
Из этих трех уравнений находим неизвестные величины
При этом всюду мы выбрали положительный знак корня. Подставляя значения
Эти формулы носят название преобразований Лоренца. Формулы обратного преобразования от штрихованных к не штрихованным величинам:
Преобразования Лоренца приводят к выводам, коренным образом противоречащим привычным представлениям о свойствах времени и пространства, сложившимся на основе повседневного опыта. Рассмотрим несколько примеров применения преобразований Лоренца. 6.2. Одновременность событий в разных системах отсчета. Пусть в системе K в точках с координатами
и моменты времени
где Из написанных формул видно, что в случае, если события в системе K происходят в одном и том же месте пространства Если же события в системе K пространственно разобщены Причинно связанные события (например, выстрел и попадание пули в мишень) ни в одной системе отсчета не будут одновременными и во всех системах событие, являющееся причиной, будет предшествовать следствию. 6.3. Длина тел в разных системах. Рассмотрим стержень, расположенный вдоль оси х и покоящийся относительно системы K' . Длина его в этой системе равна:
откуда
или, окончательно
Таким образом, длина стержня Скорости, при которых сокращение размеров движущихся материальных 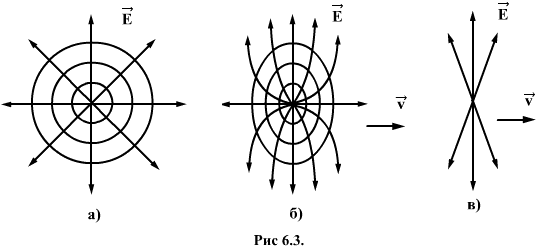 тел становится заметным, носят название релятивистских скоростей, и в настоящее время они достигнуты в крупных масштабах в лабораторной практике и в новых промышленных аппаратах. В ядерных реакторах атомныхэлектростанций быстрые нейтроны движутся со скоростями, для которых Любопытно, что визуально (или на фотографии) изменение формы тела даже при сравнимых со скоростью света скоростях, не может быть обнаружено. Причина этого весьма проста. Наблюдая визуально или фотографируя какое-либо тело, мы регистрируем импульсы света от разных участков тела достигшие одновременно сетчатки глаза или фотопластинки. Испускаются же эти импульсы не одновременно. Импульсы от более удаленных участков тела были испущены раньше, чем от более близких участков. Таким образом, если тело движется, на сетчатке глаза получается искаженное изображение тела. Соответствующий расчет показывает, что следствием искажения будет уничтожение лоренцевого сокращения, так что тела кажутся не искаженными, а лишь повернутыми. Если бы лоренцевого сокращения не было, тела казались бы вытянутыми в направлении движения. 6.4. Длительность событий в разных системах отсчета. Пусть в точке х', неподвижной относительно системы K', происходит событие длящееся время
Откуда
или
Время
Именно настолько постареют люди на Земле к моменту возвращения космонавтов. С другой стороны, по часам, установленным на космическом корабле, полет займет меньшее время
В соответствии с принципом относительности все процессы на космическом корабле (в том числе и процесс старения космонавтов) идут так же, как и на Земле, но не по земным часам, а по часам, установленным на корабле. Пусть, например,
6.5. Релятивистский закон сложения скоростей. Пусть в системе отсчета K' материальная точка движется вдоль оси х' спостоянной скоростью
Подставляя
Делим числитель и знаменатель на t
Это равенство выражает собой релятивистский закон сложения скоростей. При малых значениях скоростей
т.е. релятивистский закон сложения скоростей переходит в классический
6.6. Релятивистский импульс.Уравнения классической механики инвариантны по отношению к преобразованиям Галилея, по отношению же к преобразованиям Лоренца они оказываются неинвариантными. Из теории относительности следует, что уравнение динамики, инвариантное по отношению к преобразованиям Лоренца, имеет вид:
где
Мы приходим к выводу, что релятивистский импульс частицы равен
2.2. Релятивистская масса. Определив массу частицы m как коэффициент пропорциональности между скоростью и импульсом, получим, что масса частицы зависит от ее скорости.
2.3. Энергия в релятивистской динамике. Для энергии частицы в теории относительности получается выражение:
Из (2.3) следует, что покоящаяся частица обладает энергией
Эта величина носит название энергии покоя частицы. Kинетическая энергия, очевидно, равна
Приняв во внимание, что
Из последнего выражения вытекает, что энергия и масса тела всегда пропорциональны друг другу. Всякое изменение энергии тела
и, наоборот, всякое изменение массы |
 совпадает со временем в системе K, как это безоговорочно принималось в классической физике. Для просторы выкладок выберем направление скорости за направление осей х и
совпадает со временем в системе K, как это безоговорочно принималось в классической физике. Для просторы выкладок выберем направление скорости за направление осей х и 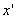 . Предположим, что в некоторый момент времени t' в точке скоординатами
. Предположим, что в некоторый момент времени t' в точке скоординатами 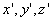 происходит некоторый физический процесс, который назовем событием. Нашей задачей является нахождение «координат» события в системе отсчета K', т.е. нахождение величин х, y, z, t, характеризующих тот же физический процесс в системе K.
происходит некоторый физический процесс, который назовем событием. Нашей задачей является нахождение «координат» события в системе отсчета K', т.е. нахождение величин х, y, z, t, характеризующих тот же физический процесс в системе K.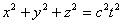
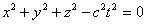
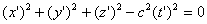
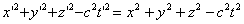
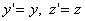
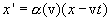
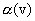 может зависеть лишь от скорости относительного движения. Не делая никаких произвольных допущений о совпадении времени в двух системах отсчета, мы можем представить t' в виде линейной однородной функции х и t
может зависеть лишь от скорости относительного движения. Не делая никаких произвольных допущений о совпадении времени в двух системах отсчета, мы можем представить t' в виде линейной однородной функции х и t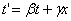
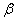 и
и 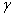 могут, вообще говоря, зависеть от скорости v. Если бы оказалось, что
могут, вообще говоря, зависеть от скорости v. Если бы оказалось, что 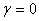 , а
, а 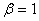 , то мы вернулись бы к преобразованиям Галилея. Для определения коэффициентов
, то мы вернулись бы к преобразованиям Галилея. Для определения коэффициентов 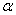 ,
, 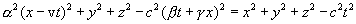
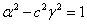
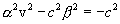
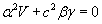
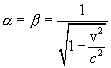
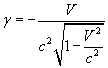

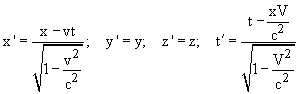
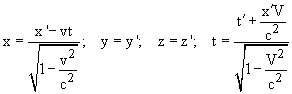
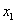 и
и 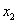 происходят одновременно два события в момент времени
происходят одновременно два события в момент времени 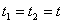 . Согласно преобразованиям Лоренца в системе K' этим событиям будут соответствовать координаты
. Согласно преобразованиям Лоренца в системе K' этим событиям будут соответствовать координаты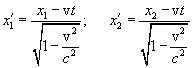
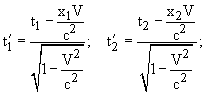
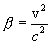
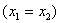 , то они будут совпадать в пространстве
, то они будут совпадать в пространстве 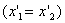 и во времени
и во времени 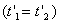 также в системе K'.
также в системе K'.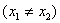 , но будут одновременными. Знак разности
, но будут одновременными. Знак разности 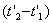 определяется знаком выражения
определяется знаком выражения 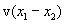 . Из этого следует, что в разных системах
. Из этого следует, что в разных системах 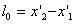 , где
, где 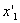 и
и 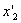 - не изменяющиеся со временем
- не изменяющиеся со временем 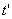 координаты концов стержня. Относительно системы K стержень движется со скоростью v. Для определения его длины в этой системе нужно отметить координаты концов стержня
координаты концов стержня. Относительно системы K стержень движется со скоростью v. Для определения его длины в этой системе нужно отметить координаты концов стержня 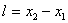 даст длину стержня, измеренную в системе K. Чтобы найти соотношение между
даст длину стержня, измеренную в системе K. Чтобы найти соотношение между 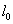 и
и 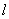 , следует взять ту из формул преобразования Лоренца, которая содержит
, следует взять ту из формул преобразования Лоренца, которая содержит 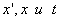 , т.е.
, т.е.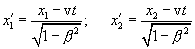
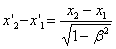
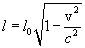
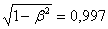 , т.е. сокращение длины порядка 0,3%. Релятивистские частицы, приходящих на Землю космических лучей имеют
, т.е. сокращение длины порядка 0,3%. Релятивистские частицы, приходящих на Землю космических лучей имеют 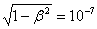 и продольные размеры сокращаются в 10 миллионов раз. Для быстро летящих заряженных частиц подобной продольной деформации подвергается сопровождающее их электромагнитное поле. На рис.6.За изображены линии поля и постоянного потенциала
и продольные размеры сокращаются в 10 миллионов раз. Для быстро летящих заряженных частиц подобной продольной деформации подвергается сопровождающее их электромагнитное поле. На рис.6.За изображены линии поля и постоянного потенциала 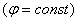 электрического поля точечного заряда, когда он неподвижен. На рис. 6.36 тот же заряд, движущийся с не слишком большой скоростью, на рис.6.3в - со скоростью, очень близкой скорости света. Если в первом случае поле сферически симметрично, то в последнем оно практически сжимается в «лепешку», перпендикулярную к направлению движения. Эту деформацию электромагнитного поля можно обнаружить на опыте. Релятивистская частица будет взаимодействовать с неподвижным пробным зарядом
электрического поля точечного заряда, когда он неподвижен. На рис. 6.36 тот же заряд, движущийся с не слишком большой скоростью, на рис.6.3в - со скоростью, очень близкой скорости света. Если в первом случае поле сферически симметрично, то в последнем оно практически сжимается в «лепешку», перпендикулярную к направлению движения. Эту деформацию электромагнитного поля можно обнаружить на опыте. Релятивистская частица будет взаимодействовать с неподвижным пробным зарядом 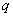 , помещенным на ее пути, лишь в течении очень краткого времени, когда «лепешка» силовых линий проходит через заряд
, помещенным на ее пути, лишь в течении очень краткого времени, когда «лепешка» силовых линий проходит через заряд 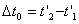 . Началу события соответствует в этой системе координата
. Началу события соответствует в этой системе координата 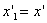 и момент времени
и момент времени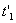 , концу события - координата
, концу события - координата 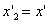 и момент времени
и момент времени 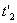 . Относительно системы K точка, в которой происходит событие, перемещается. Согласно преобразованиям Лоренца началу и концу события соответствуют в системе K'.
. Относительно системы K точка, в которой происходит событие, перемещается. Согласно преобразованиям Лоренца началу и концу события соответствуют в системе K'.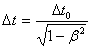
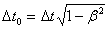
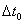 , отсчитанное по часам, движущимся вместе с телом, называют собственным временем этого тела. Kак видно из уравнения, собственное время всегда меньше, чем время, отсчитанное по часам, движущимся относительно тела.Релятивистский эффект замедления хода времени позволяет в принципе осуществить «путешествие в будущее» (но не в прошлое). В самом деле, пусть космический корабль, движущийся со скоростью
, отсчитанное по часам, движущимся вместе с телом, называют собственным временем этого тела. Kак видно из уравнения, собственное время всегда меньше, чем время, отсчитанное по часам, движущимся относительно тела.Релятивистский эффект замедления хода времени позволяет в принципе осуществить «путешествие в будущее» (но не в прошлое). В самом деле, пусть космический корабль, движущийся со скоростью 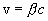 (где
(где 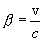 ) относительно Земли, совершает перелет от Земли до некоторой звезды и обратно. Если свет проходит путь
) относительно Земли, совершает перелет от Земли до некоторой звезды и обратно. Если свет проходит путь 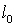 от звезды до Земли за время
от звезды до Земли за время 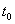 , то
, то 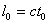 и для земного наблюдателя продолжительность перелета равна:
и для земного наблюдателя продолжительность перелета равна: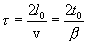
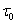 , которое:
, которое: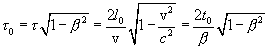
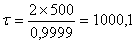 лет, а
лет, а 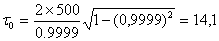 лет.
лет.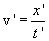 Система K' движется относительно системы K в том же направлении со скоростью v , Определим, чему равна скорость материальной точки vo, относительно системы K, т.е. чему равно
Система K' движется относительно системы K в том же направлении со скоростью v , Определим, чему равна скорость материальной точки vo, относительно системы K, т.е. чему равно 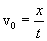 . Пусть при
. Пусть при 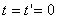 м.т. находится в начале координат, причем
м.т. находится в начале координат, причем 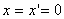 . Для системы K:
. Для системы K: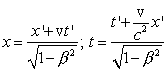
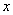 и t в формулу для vo
и t в формулу для vo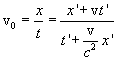
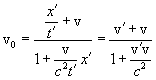
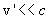 и
и 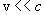 имеем
имеем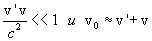
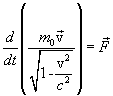
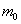 - инвариантная, т.е. одинаковая во всех системах отсчета величина называемая массой покоя частицы, v- скорость частицы,
- инвариантная, т.е. одинаковая во всех системах отсчета величина называемая массой покоя частицы, v- скорость частицы, 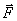 - сила действующая на частицу. Сопоставим с классическим уравнением
- сила действующая на частицу. Сопоставим с классическим уравнением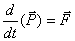
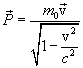
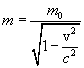
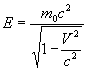
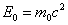
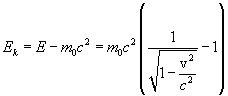
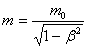 , выражение для полной энергии частицы можно написать в виде
, выражение для полной энергии частицы можно написать в виде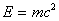
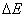 сопровождается изменением массы тела
сопровождается изменением массы тела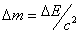
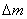 сопровождается изменениемэнергии
сопровождается изменениемэнергии 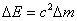 . Это утверждение носит название закона взаимосвязи или закона пропорциональности массы и энергии.
. Это утверждение носит название закона взаимосвязи или закона пропорциональности массы и энергии.