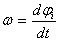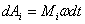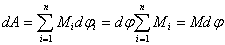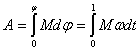|
В динамике поступательного движения материальной точки были введены в дополнение к кинематическим величинам, понятия силы и массы. Аналогично, для изучения динамики вращательного движения тела, помимо рассмотренных кинематических характеристик, вводятся новые величины - момент силы, момент инерции и момент импульса.
5.1. Особенности вращательного движения.
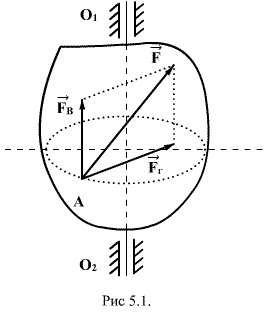
Рассмотрим движение твердого тела, имеющею ось вращения 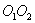 под действием произвольно направленной силы под действием произвольно направленной силы 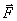 , приложенной к телу в некоторой точке А , которую можно разложить на две составляющие: вертикальную и горизонтальную (рис.5.1). Вертикальная составляющая может вызывать перемещение тела в направлении оси вращения поэтому при рассмотрении вращательного движения ее можно исключить.Горизонтальная составляющая , приложенной к телу в некоторой точке А , которую можно разложить на две составляющие: вертикальную и горизонтальную (рис.5.1). Вертикальная составляющая может вызывать перемещение тела в направлении оси вращения поэтому при рассмотрении вращательного движения ее можно исключить.Горизонтальная составляющая 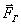 , если она не пересекается с осью , если она не пересекается с осью 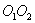 вызывает вращение тела. Действие этой силы зависит от ее числового значения и расстояния линии действия от оси вращения. вызывает вращение тела. Действие этой силы зависит от ее числового значения и расстояния линии действия от оси вращения.
5.2. Вращающий момент (или момент силы.)
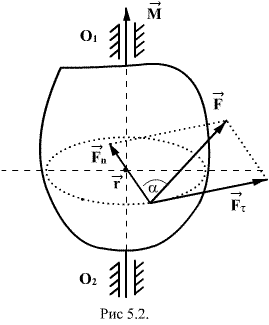
Пусть на тело, в плоскости перпендикулярной оси вращения 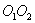 действует сила действует сила 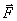 (рис.5.2). Разложим эту силу на две составляющие: (рис.5.2). Разложим эту силу на две составляющие: 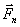 и и 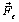
Сила 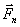 пересекает ось вращения и, следовательно, не влияет на вращение тела. Под действием составляющей пересекает ось вращения и, следовательно, не влияет на вращение тела. Под действием составляющей 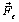 тело будет совершать вращательное движение вокруг оси тело будет совершать вращательное движение вокруг оси 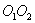 . Расстояние . Расстояние 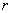 от оси вращения до линии вдоль которой действует сила от оси вращения до линии вдоль которой действует сила 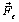 называется плечом силы называется плечом силы 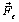 . Моментом силы относительно точки О называется произведение модуля силы . Моментом силы относительно точки О называется произведение модуля силы 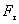 на плечо на плечо 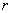
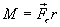
С учетом, что 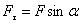
момент силы
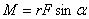 . .
С точки зрения векторной алгебры это выражение представляет векторное произведение радиуса-вектора 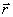 , проведенного в точку приложения силы , проведенного в точку приложения силы 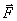 на эту силу. Таким образом, момент силы относительно точки О является векторной величиной и равен на эту силу. Таким образом, момент силы относительно точки О является векторной величиной и равен
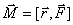 |
(5.1) |
Вектор момента силы направлен перпендикулярно к плоскости, проведенной через векторы 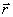 и и 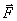 , и образует с ними правую тройку векторов (при наблюдении из вершины вектора М видно, что вращение по кратчайшему расстоянию от , и образует с ними правую тройку векторов (при наблюдении из вершины вектора М видно, что вращение по кратчайшему расстоянию от 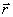 к к 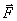 происходит против часовой стрелки). происходит против часовой стрелки).
5.3. Момент инерции материальной точки относительно неподвижной оси вращения.
Согласно второму закону Ньютона, для тангенциальной составляющейсилы 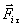 , действующей на материальную точку массой m, и ускорения , действующей на материальную точку массой m, и ускорения 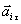
можем записать
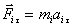
С учетом, что
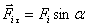 и и 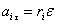
имеем
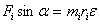
Домножимлевую и правую части на 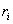 и получим и получим
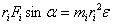 |
(5.2) |
или
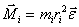
Произведение массы материальной точки 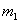 тела на квадрат ее расстояния тела на квадрат ее расстояния 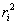 до оси вращения называется моментом инерции материальной точки относительно оси вращения: до оси вращения называется моментом инерции материальной точки относительно оси вращения:
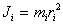 |
(5.3) |
5.4. Момент инерции твердого тела
Чтобы найти момент инерции тела, надо просуммировать момент инерции всех материальных точек, составляющих данное тело
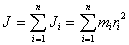 |
(5.4) |
В общем случае, если тело сплошное, оно представляет собой совокупность множества точек с бесконечно малыми массами 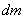 , и моменты инерции тела определяется интегралом , и моменты инерции тела определяется интегралом
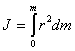 |
(5.5) |
о где 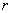 - расстояние от элемента - расстояние от элемента 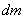 до оси вращения. до оси вращения.
Распределение массы в пределах тела можно охарактеризовать с помощью
плотности
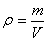 |
(5.5) |
где m - масса однородного тела, V - его объем. Для тела с неравномерно распределенной массой это выражение даетсреднюю плотность.
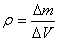
Плотность в данной точке в этом случае определяется следующим образом
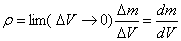
и тогда
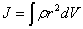 |
(5.6) |
Пределы интегрирования зависят от формы и размеров тела Интегрирование уравнения (5.5) наиболее просто осуществить для тех случаев, когда ось вращения проходит через центр тяжести тела. Рассмотрим результаты интегрирования для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.
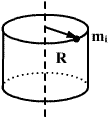
Момент инерции полого цилиндра с тонкими стенками, радиуса R.
Для полого цилиндра с тонкими стенками
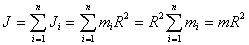
Сплошной однородный диск. Ось вращения является осью диска радиуса 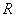 . и массы m с плотностью . и массы m с плотностью 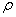 Высота диска h. Внутри диска на расстоянии вырежем пустотелый цилиндр с толщиной стенки Высота диска h. Внутри диска на расстоянии вырежем пустотелый цилиндр с толщиной стенки 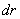 и массой и массой 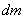 . Для него . Для него
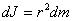
Весь диск можно разбить на бесконечное множество цилиндров, а затем просуммировать:
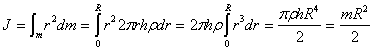
Момент инерции шара относительно оси, проходящей через центр тяжести.
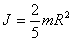
Момент инерции стержня длиной L и массой m относительно оси, проходящей:
а) через центр стержня - 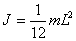
б) через начало стержня - 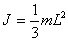
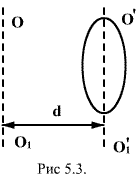
Теорема Штейнера. Имеем тело, момент инерции которого относительно оси, проходящей через его центр масс 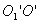 известен. Необходимо определить момент инерции относительно произвольно оси известен. Необходимо определить момент инерции относительно произвольно оси 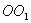 параллельной оси параллельной оси 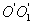 . Согласно теореме Штейнера, момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, плюс произведение массы тела на квадрат расстояния между осями: . Согласно теореме Штейнера, момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, плюс произведение массы тела на квадрат расстояния между осями:
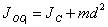 |
(5.7) |
5.5. Второй закон Ньютона для вращательного движения и его анализ.
С учетом (5.2) и (5.3) вращающий момент тела
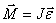 |
(5.8) |
или
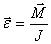
Это выражение представляет собой аналог второго закона Ньютона для вращательного движения, из которого следует, что угловое ускорение 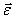 твердого тела при вращении вокруг неподвижной оси прямо пропорционально вращающему моменту и обратно пропорционально моменту инерции Относительно этой оси. Из этого выражения следует, что момент инерции U является мерой его инертности во вращательном движении вокруг неподвижной оси. В случае поступательного движения мерой инертности, как известно, является масса тела. твердого тела при вращении вокруг неподвижной оси прямо пропорционально вращающему моменту и обратно пропорционально моменту инерции Относительно этой оси. Из этого выражения следует, что момент инерции U является мерой его инертности во вращательном движении вокруг неподвижной оси. В случае поступательного движения мерой инертности, как известно, является масса тела.
5.6. Момент импульса материальной точки и твердого тела.
Векторное произведение радиуса-вектора 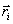 материальной точки на ее импульс: материальной точки на ее импульс: 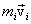 называют моментом импульса называют моментом импульса 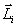 , этой точки относительно точки О (рис.5.4) , этой точки относительно точки О (рис.5.4)
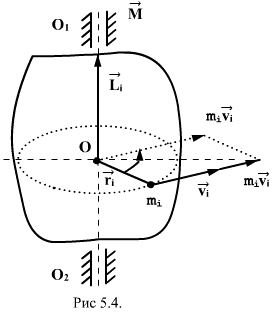
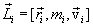 . Вектор . Вектор 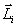 иногда называют также моментом количества движения материальной точки. Он направлен вдоль оси вращения перпендикулярно плоскости, проведенной через векторы иногда называют также моментом количества движения материальной точки. Он направлен вдоль оси вращения перпендикулярно плоскости, проведенной через векторы 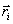 и и 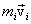 и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от и образует с ними правую тройку векторов (при наблюдении из вершины вектора видно, что вращение по кратчайшему расстоянию от 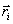 к к 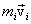 происходит против часовой стрелки). происходит против часовой стрелки).
Векторную сумму моментов импульсов 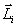 всех материальных точек системы называют моментом импульса (количества движения) всех материальных точек системы называют моментом импульса (количества движения) 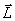 системы относительно точки О: системы относительно точки О:
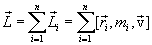
Векторы 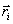 и и 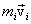 взаимно перпендикулярны и лежат в плоскости перпендикулярной оси вращения тела. Поэтому взаимно перпендикулярны и лежат в плоскости перпендикулярной оси вращения тела. Поэтому 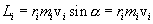 . Сучетом связи линейных и угловых величин . Сучетом связи линейных и угловых величин
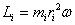
и направлен вдоль оси вращения тела в ту же сторону, что и вектор 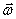 . .
Таким образом.
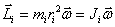
Момент импульса тела относительно оси вращения
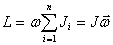
т.е.
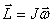 |
(5.9) |
Следовательно, момент импульса тела относительно оси вращения равен произведению момента инерции тела относительно той же оси на угловую скорость вращения тела вокруг этой оси.
5.7. Основное уравнение динамики вращательного движения.
Согласно уравнению (5.8) второй закон Ньютона для вращательного движения
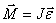
По определению угловое ускорение 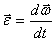 и тогда это уравнение можно и тогда это уравнение можно
переписать следующим образом
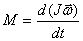
с учетом (5.9)
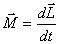
или
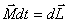 |
(5.10) |
Это выражение носит название основного уравнения динамики вращательного движения и формулируется следующим образом: изменение момента количества движения твердого тела 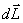 , равно импульсу момента , равно импульсу момента 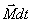 всех внешних сил, действующих на это тело. всех внешних сил, действующих на это тело.
5.8. Закон сохранения момента количества движения.
Из основного уравнения динамики вращательного движения следует, что
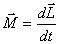
Для замкнутой (изолированной) системы результирующий вектор момента 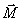 всех внешних сил, действующих на тело, равен нулю и всех внешних сил, действующих на тело, равен нулю и
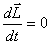
или
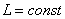
Это утверждение представляет собой содержание закона сохранения момента количества движения: и формулируется следующим образом: если результирующий момент всех внешних сил относительно неподвижной осивращения тела равен нулю, то момент импульса относительно этой оси не изменяется в процессе движения. Этот закон может быть обобщен на любую незамкнутую систему тел, если результирующий момент всех внешних сил, приложенных к системе, относительно какой-либо неподвижной оси тождественно равен нулю, то момент импульса системы относительно той же оси не изменяется с течением времени.
Пример.
Вал в виде сплошного цилиндра массой 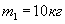 надет на горизонтальную ось. На цилиндр накручена нить, к свободному концу которой подвешена гиря массой надет на горизонтальную ось. На цилиндр накручена нить, к свободному концу которой подвешена гиря массой 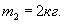 Определить ускорение, с которым опускается гиря. Определить ускорение, с которым опускается гиря.
Решение.
Линейное ускорение 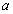 гири равно тангенциальному ускорению точек вала, которые лежат на его поверхности, и связано с угловым ускорением вала соотношением гири равно тангенциальному ускорению точек вала, которые лежат на его поверхности, и связано с угловым ускорением вала соотношением
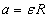 , ,
где 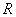 -радиус вала. -радиус вала.
Угловое ускорение вала можно найти из основного уравнения динамики вращательного движения
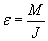 , ,
где 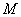 -момент силы, действующей на вал; -момент силы, действующей на вал; 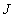 - момент инерции вала. - момент инерции вала.
Момент инерции вала относительно геометрической оси равен
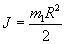 . .
Вращающий момент, действующий на вал, равен произведению силы натяжения нити на радиус вала:
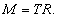
Силу натяжения нити найдем из второго закона Ньютона:
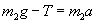 , ,
откуда
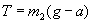 . .
Таким образом, вращающий момент
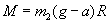 . .
Подставляем в формулу для 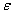 выражения для выражения для 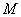 и и 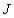 , тогда , тогда
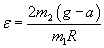 . .
Учитывая то, что 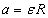 ![endif]> , получим ![endif]> , получим
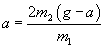 , ,
откуда получим окончательный результат
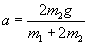 . .
5.9. Гироскоп. Гироскопический эффект.
Гироскопом (или волчком) называют массивное симметричное тело, вращающееся с большой скоростью вокруг оси симметрии (рис.5.5).
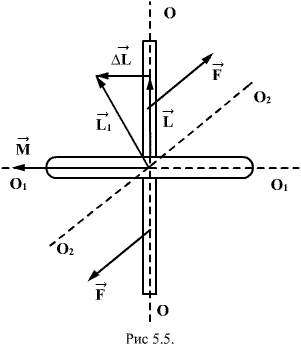
Момент количества движения гироскопа совпадает с его осью вращения. Для того, чтобы изменитьнаправление в пространстве оси гироскопа, т.е. направление вектора 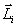 необходимо в соответствие основным уравнением динамики вращательного движения необходимо в соответствие основным уравнением динамики вращательного движения 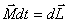 подействовать на него моментом внешних сил подействовать на него моментом внешних сил 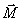 . Пусть это пара сил . Пусть это пара сил 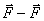 создающая вращающий момент относительно оси создающая вращающий момент относительно оси 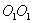 , лежащей в плоскости чертежа перпендикулярно оси ОО (вращение вокруг , лежащей в плоскости чертежа перпендикулярно оси ОО (вращение вокруг 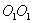 ). При этом наблюдается следующее явление, получившее название гироскопического эффекта: под действием пары сил, которые, казалось бы, должны были вызвать поворот оси гироскопа ОО вокруг оси ). При этом наблюдается следующее явление, получившее название гироскопического эффекта: под действием пары сил, которые, казалось бы, должны были вызвать поворот оси гироскопа ОО вокруг оси 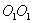 , ось гироскопа поворачивается вокруг прямой , ось гироскопа поворачивается вокруг прямой 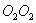 перпендикулярно к этим осям (т.е. к ОО и перпендикулярно к этим осям (т.е. к ОО и 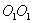 ). «Противоестественное» на первый взгляд поведение гироскопа оказывается, как легко видеть, полностью соответствует законам динамики вращательного движения, т.е. в конечном счете, законам Ньютона. Рассмотрим поведение гироскопа под действием момента силы ). «Противоестественное» на первый взгляд поведение гироскопа оказывается, как легко видеть, полностью соответствует законам динамики вращательного движения, т.е. в конечном счете, законам Ньютона. Рассмотрим поведение гироскопа под действием момента силы 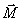 действующего вдоль оси действующего вдоль оси 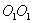 . За время . За время 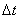 момент количества движения гироскопа момент количества движения гироскопа 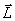 получит приращение получит приращение 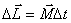 , которое имеет такое же направление, как и , которое имеет такое же направление, как и 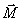 . Момент количества движения гироскопа спустя время . Момент количества движения гироскопа спустя время 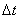 будет равен результирующей будет равен результирующей 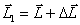 , лежащей в плоскости чертежа. Направление вектора , лежащей в плоскости чертежа. Направление вектора 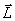 совпадает с новым направлением оси вращения гироскопа. Таким образом, ось гироскопа повернется вокруг оси совпадает с новым направлением оси вращения гироскопа. Таким образом, ось гироскопа повернется вокруг оси 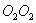 (перпендикулярной плоскости чертежа), причем так, что угол между векторами (перпендикулярной плоскости чертежа), причем так, что угол между векторами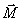 и и 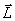 уменьшится: Если действовать на гироскоп длительное время постоянным по направлению моментом внешних сил, то ось гироскопа устанавливается в конце концов так, что ось и направление собственного вращения совпадают с осью и направлением вращения под действием внешних сил (вектор уменьшится: Если действовать на гироскоп длительное время постоянным по направлению моментом внешних сил, то ось гироскопа устанавливается в конце концов так, что ось и направление собственного вращения совпадают с осью и направлением вращения под действием внешних сил (вектор 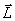 , совпадает по направлению с вектором , совпадает по направлению с вектором 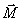 ). ).
5.10. Кинетическая энергия вращающегося тела
Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:
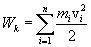
Если тело вращается вокруг неподвижной оси с угловой скоростью 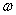 , то линейная скорость i-ой точки равна , то линейная скорость i-ой точки равна 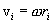 , где , где 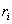 , - расстояние от этой точки до оси вращения. Следовательно. , - расстояние от этой точки до оси вращения. Следовательно.
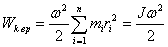 |
(5.11) |
где 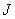 - момент инерции тела относительно оси вращения. - момент инерции тела относительно оси вращения.
В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости 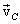 центра инерции тела, и вращения с угловой скоростью центра инерции тела, и вращения с угловой скоростью 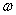 вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду
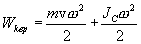 |
(5.12) |
где 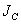 - момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции. - момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.
5.11. Работа внешних сил при вращении твердого тела.
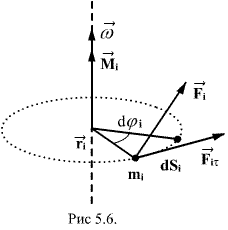
Рассмотрим действие внешней силы 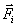 , приложенной к точке массой , приложенной к точке массой 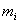 . За время . За время 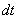 элементарная масса элементарная масса 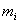 проходит путь проходит путь 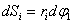 Работа силы Работа силы 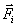 на этом пути определяется проекцией силы на направление перемещения, которая очевидно, равна тангенциальной составляющей на этом пути определяется проекцией силы на направление перемещения, которая очевидно, равна тангенциальной составляющей 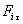 силы. силы.
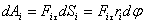
Но 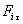 равна модулю момента равна модулю момента 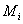 силы силы 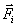 относительно оси вращения. Работа относительно оси вращения. Работа 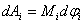 , и будет положительна, если , и будет положительна, если 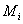 имеет такое же направление, как и имеет такое же направление, как и 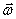 отрицательное, если направление векторов отрицательное, если направление векторов 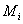 и и 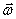 противоположны. противоположны.
С учетом, что 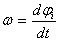
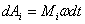
Работа всех сил, приложенных к телу
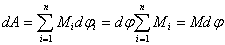 |
(5.13) |
Полная работа
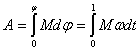 |
(5.14) |
|





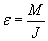 ,
,
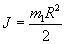
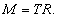
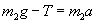
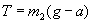
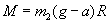
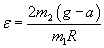
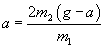
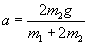


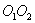 под действием произвольно направленной силы
под действием произвольно направленной силы 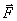 , приложенной к телу в некоторой точке А , которую можно разложить на две составляющие: вертикальную и горизонтальную (рис.5.1). Вертикальная составляющая может вызывать перемещение тела в направлении оси вращения поэтому при рассмотрении вращательного движения ее можно исключить.Горизонтальная составляющая
, приложенной к телу в некоторой точке А , которую можно разложить на две составляющие: вертикальную и горизонтальную (рис.5.1). Вертикальная составляющая может вызывать перемещение тела в направлении оси вращения поэтому при рассмотрении вращательного движения ее можно исключить.Горизонтальная составляющая 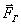 , если она не пересекается с осью
, если она не пересекается с осью 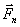 и
и 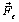
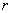 от оси вращения до линии вдоль которой действует сила
от оси вращения до линии вдоль которой действует сила 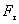 на плечо
на плечо 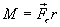
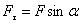
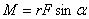 .
.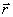 , проведенного в точку приложения силы
, проведенного в точку приложения силы 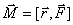
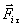 , действующей на материальную точку массой m, и ускорения
, действующей на материальную точку массой m, и ускорения 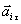
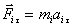
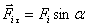 и
и 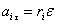
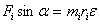
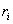 и получим
и получим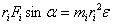
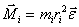
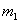 тела на квадрат ее расстояния
тела на квадрат ее расстояния 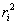 до оси вращения называется моментом инерции материальной точки относительно оси вращения:
до оси вращения называется моментом инерции материальной точки относительно оси вращения: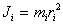
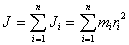
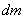 , и моменты инерции тела определяется интегралом
, и моменты инерции тела определяется интегралом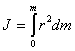
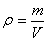
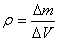
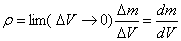
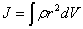
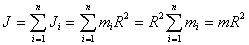
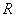 . и массы m с плотностью
. и массы m с плотностью 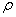 Высота диска h. Внутри диска на расстоянии вырежем пустотелый цилиндр с толщиной стенки
Высота диска h. Внутри диска на расстоянии вырежем пустотелый цилиндр с толщиной стенки 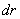 и массой
и массой 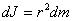
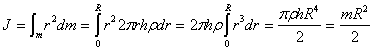
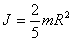
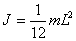
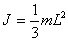
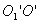 известен. Необходимо определить момент инерции относительно произвольно оси
известен. Необходимо определить момент инерции относительно произвольно оси 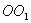 параллельной оси
параллельной оси 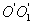 . Согласно теореме Штейнера, момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, плюс произведение массы тела на квадрат расстояния между осями:
. Согласно теореме Штейнера, момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, плюс произведение массы тела на квадрат расстояния между осями: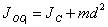
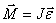
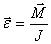
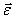 твердого тела при вращении вокруг неподвижной оси прямо пропорционально вращающему моменту и обратно пропорционально моменту инерции Относительно этой оси. Из этого выражения следует, что момент инерции U является мерой его инертности во вращательном движении вокруг неподвижной оси. В случае поступательного движения мерой инертности, как известно, является масса тела.
твердого тела при вращении вокруг неподвижной оси прямо пропорционально вращающему моменту и обратно пропорционально моменту инерции Относительно этой оси. Из этого выражения следует, что момент инерции U является мерой его инертности во вращательном движении вокруг неподвижной оси. В случае поступательного движения мерой инертности, как известно, является масса тела.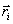 материальной точки на ее импульс:
материальной точки на ее импульс: 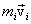 называют моментом импульса
называют моментом импульса 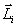 , этой точки относительно точки О (рис.5.4)
, этой точки относительно точки О (рис.5.4)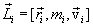 . Вектор
. Вектор 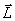 системы относительно точки О:
системы относительно точки О: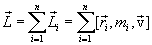
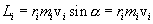 . Сучетом связи линейных и угловых величин
. Сучетом связи линейных и угловых величин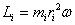
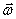 .
.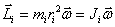
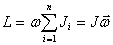
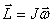
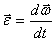 и тогда это уравнение можно
и тогда это уравнение можно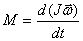
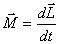
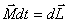
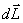 , равно импульсу момента
, равно импульсу момента 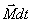 всех внешних сил, действующих на это тело.
всех внешних сил, действующих на это тело.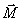 всех внешних сил, действующих на тело, равен нулю и
всех внешних сил, действующих на тело, равен нулю и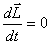
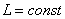
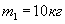 надет на горизонтальную ось. На цилиндр накручена нить, к свободному концу которой подвешена гиря массой
надет на горизонтальную ось. На цилиндр накручена нить, к свободному концу которой подвешена гиря массой 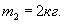
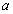
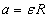 ,
,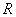 -радиус вала.
-радиус вала.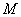 -момент силы, действующей на вал;
-момент силы, действующей на вал; 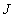 - момент инерции вала.
- момент инерции вала.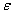
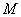
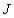 , тогда
, тогда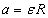 ![endif]>
![endif]>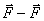 создающая вращающий момент относительно оси
создающая вращающий момент относительно оси 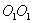 , лежащей в плоскости чертежа перпендикулярно оси ОО (вращение вокруг
, лежащей в плоскости чертежа перпендикулярно оси ОО (вращение вокруг 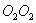 перпендикулярно к этим осям (т.е. к ОО и
перпендикулярно к этим осям (т.е. к ОО и 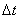 момент количества движения гироскопа
момент количества движения гироскопа 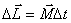 , которое имеет такое же направление, как и
, которое имеет такое же направление, как и 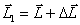 , лежащей в плоскости чертежа. Направление вектора
, лежащей в плоскости чертежа. Направление вектора 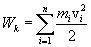
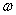 , то линейная скорость i-ой точки равна
, то линейная скорость i-ой точки равна 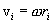 , где
, где 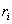 , - расстояние от этой точки до оси вращения. Следовательно.
, - расстояние от этой точки до оси вращения. Следовательно.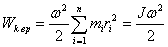
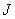 - момент инерции тела относительно оси вращения.
- момент инерции тела относительно оси вращения.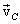 центра инерции тела, и вращения с угловой скоростью
центра инерции тела, и вращения с угловой скоростью 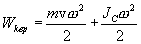
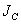 - момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.
- момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.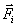 , приложенной к точке массой
, приложенной к точке массой 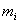 . За время
. За время 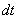 элементарная масса
элементарная масса 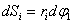 Работа силы
Работа силы 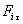 силы.
силы.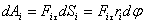
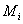 силы
силы 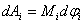 , и будет положительна, если
, и будет положительна, если